In each issue of Wharton Magazine, we’ll test your knowledge with a question straight from an actual Wharton exam, crafted by one of the School’s esteemed faculty members. Submit the correct answer and you’ll be entered into our drawing for a fabulous prize—tuition-free attendance at a Wharton Executive Education program.
This Final Exam challenge comes from Noah Gans, the Joel S. Ehrenkranz Family Professor of Operations and Information Management. Good luck!

The Basics:
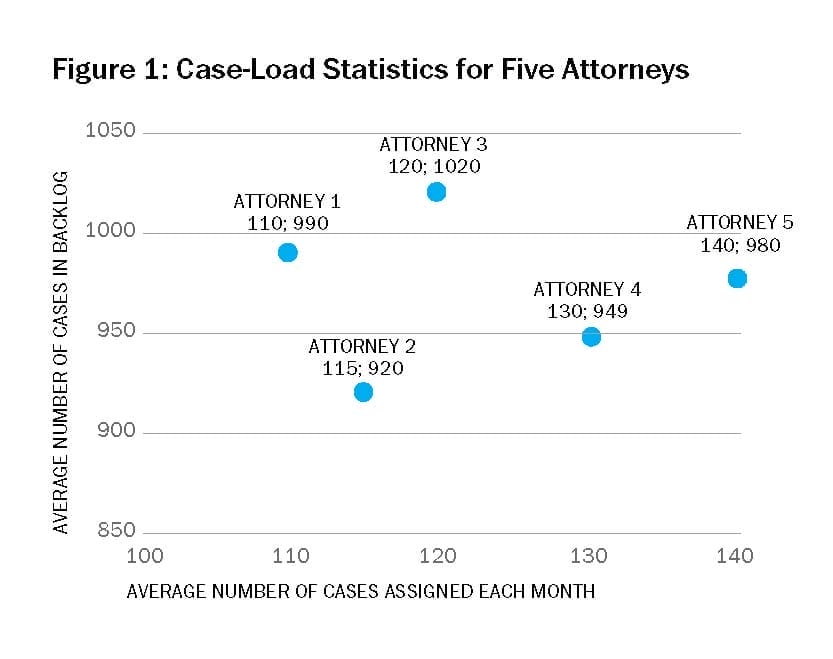
The U.S. Board of Immigration Appeals in Philadelphia has a backlog of almost 5,000 cases waiting to be processed. Each of five attorneys is assigned cases as they arrive. Figure 1 shows the number of cases assigned per month to each attorney (x-axis), as well as the average number of cases in each attorney’s backlog (y-axis).
The Question:
Assume that the arrival rate of cases to the board is fairly constant over time and that the success rate of appeals is the same across attorneys. Based on the data shown in Figure 1, if you had an immigration appeal pending before the court and wanted to minimize the expected delay before the case is heard, to which of the five attorneys would you hope it would be assigned? Why?
The Answer:
We can use the data from Figure 1 and Little’s Law (L = l·W, or I = R·T) to calculate each attorney’s average delay:
| Attorney | 1 | 2 | 3 | 4 | 5 |
| l = average rate at which cases assigned | 110 | 115 | 120 | 130 | 140 |
| L = average backlog | 990 | 920 | 1020 | 949 | 980 |
| W = L /l = average delay | 9 | 8 | 8.5 | 7.3 | 7 |
Based on these data, Attorney 5 has the shortest average time per case. You would want Attorney 5.
Noah Gans thanks Professor Avishai Mandelbaum of the Technion, whose work motivated the exam question.
The Winner:
Winner of the fall issue Final Exam challenge: John L. Jackson, W’78